
Si può dare una connotazione fisica all'aldilà? O perlomeno inquadrarla in un contesto direzionale logico? Parliamo in questo caso di una dimensione che va oltre la nostra e come tale deve avere per forza di cose delle caratteristiche in più rispetto alle classiche tre dimensioni proprie del mondo fisico. Si cerca quindi in questo contesto una possibile quarta dimensione.
Con la definizione di quarta dimensione ci si riferisce ad una dimensione immediatamente successiva alle tre dimensioni dello spazio reale che sono altezza, larghezza e profondità. Lo studio di questa dimensione assorbita alle tre percepite dall'uomo abbraccia non solo i campi della matematica e della fisica ma anche quello della filosofia e della psicologia e, come corollario, anche quelli della letteratura e della spiritualità.
Generalmente il tema della quarta dimensione si sdoppia in due tronconi di pensiero specifici; il primo parte dallo studio della fenomenologia naturale che avviene misurando l'evolversi del fenomeno in ampiezza, altezza, profondità e tempo. Da questo ne scaturisce che essendo le prime tre grandezze per definizione le tre dimensioni dello spazio, il tempo diventa a pieno titolo la quarta dimensione. Il secondo similmente al primo parte dall'uso delle tre dimensioni del nostro spazio; altezza, ampiezza e profondità che sono ortogonali tra loro ma tiene da parte il tempo da quest'insieme e definisce la quarta dimensione come una dimensione ortogonale alle altre tre. In pratica tale rappresentazione ideologica si riferisce al modello di spazio euclideo esteso a quattro dimensioni.
A dare origine al processo di definire una quarta dimensione fu a cavallo degli ultimi anni del diciottesimo secolo e la prima metà del diciannovesimo la ricerca da parte di alcuni scienziati riguardo la validità del quinto postulato di Euclide. Una formulazione di questo postulato dice che "date due rette parallele tagliate da una trasversale, la somma dei due angoli coniugati interni è pari ad un angolo piatto." Alcuni tra i quali annoveriamo Carl Friedrich Gauss giunsero a dimostrare che c'erano situazioni in cui tale postulato non era valido. Fu Bernhard Riemann nel 1854 con la sua tesi di dottorato a confermare che in effetti il quinto postulato non vale per uno spazio curvo. Dalla necessità di rispondere alla domanda "rispetto a che cosa si può curvare uno spazio a tre dimensioni?" si iniziò a discutere sulle possibilità di esistenza di ulteriori dimensioni dovute a fattori intrinseci come il tempo.
Questa risposta venne dal fisico Hermann Von Helmholtz che dichiarò che aveva pensato alla possibilità di spazi multidimensionali. Prendendo spunto dalla dichiarazione di Helmhotz, un suo collega di facoltà, lo psicologo e fisiologo Gustav Fechner affermò che lo spazio presenta quattro dimensioni e che la quarta dimensione era il tempo. Fu in effetti Fechner in questo racconto a dare l'avvio ad una descrizione di spazio quadrimensionale facendo un'analogia su come un essere bidimensionale potesse vedere le tre dimensioni.
La popolarizzazione dei concetti di spazi multidimensionali avvenne nel 1884 con la pubblicazione del libro "Flatlandia. Racconto fantastico a più dimensioni" scritto dall'inglese Edwin Abbott. Da questo testo prese ispirazione anche Gaston De Pawlowsky che nel 1912 pubblicò interamente la sua opera intitolata "Voyage au Pays de la Quatrième Dimension."
Con la definizione della relatività da parte di Albert Einstein nel 1905 e i successivi studi e osservazioni sul comportamento della luce sotto il campo gravitazionale prodotto dal Sole, nel 1908 si ottennero fondati motivi per ritenere che la quarta dimensione non era solo un concetto teorico ma anche una realtà. Einstein stesso in quel periodo ideò il modello di spazio quadrimensionale in cui la quarta dimensione era il tempo.
Nel 1908 il matematico tedesco Hermann Minkowski servendosi di nozioni di geometrie non euclidee perfezionò un modello spaziotemporale indipendente dal sistema di riferimento. Nel 1919 il matematico polacco Theodor Kaluza, studioso della teoria della relatività di Einstein, propose un'ipotesi di quarta dimensione invisibile perché in qualche modo limitata in dimensioni microscopiche. Kaluza propose ad Einstein questa sua idea e questi ne riconobbe la sua originalità nel 1921. Kaluza ed Einstein cercarono di approfondire tale teoria di dimensione extraspaziale ma solo nel 1926 il matematico svedese Oskar Klein riuscì ad approfondire quel modello di quarta dimensione. Klein propose una quarta dimensione arrotolata in modo da costituire un cerchio intorno ad ogni punto fisico dello spazio. Tale cerchio avrebbe avuto un diametro di 10-33 cm cioè pari alla lunghezza di Plank che ricordiamo descrive la distanza oltre la quale il concetto di dimensione perde ogni significato fisico.
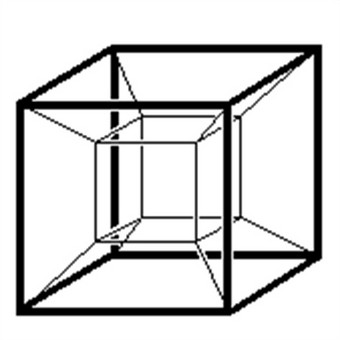
Il considerare il tempo come quarta dimensione discende dalla ricerca per lo studio di funzioni in fisica matematica. Infatti molti fenomeni naturali variano sia al variare della posizione nello spazio che nel tempo. Tale impostazione conduce a confermare il tempo come quarta dimensione quando si parla di spazi multidimensionali con più di quattro dimensioni. Tempo e spazio sono due concetti diversi. Se definissimo la quarta dimensione come il tempo allora il tempo si interpreterebbe come uno spazio, cosa che non è. Pensiamo ad un qualsiasi oggetto tridimensionale e facciamolo muovere. Il movimento di un solido non ci fa ottenere altri riferimenti spaziali se non la profondità, l'altezza e la base. In geometria Euclidea un punto definito su uno spazio a quattro dimensioni ha quattro coordinate e le coordinate non sono espresse da secondi, minuti od ore, bensì da lunghezze spaziali.
La Quarta Dimensione quindi è intorno a noi tutti i giorni. La quarta dimensione rappresenta semplicemente il cambiamento e la trasformazione della materia fisica che avviene grazie al fattore tempo.
Supponiamo di poter muovere una palla in un percorso dritto; questa è la Prima Dimensione, avanti e indietro.
Supponiamo ora di poter muovere la palla anche a destra o a sinistra. In questo caso ci stiamo muovendo anche nella Seconda Dimensione.
Ora immaginiamo che questa palla possa muoversi anche verso l'alto o verso il basso. In questo caso otteniamo la Terza Dimensione.
La realtà come siamo abituati a conoscerla nella vita di tutti i giorni è composta da oggetti in tre dimensioni. Noi stessi siamo materia in tre dimensioni. Ritornando all'esempio precedente la palla in uno spazio a tre dimensioni può muoversi in tutte le direzioni oltre che sul piano anche in alto e in basso. Ogni punto dello spazio ha tre dimensioni, è individuato univocamente dalle coordinate (X, Y, Z).
Ora prendiamo la palla e spingiamola verso una qualsiasi direzione in modo che rotoli da un punto A ad un punto B in un determinato lasso di tempo. Quindi la posizione della palla dipende dal tempo che passa dall'istante dello spostamento (T) fino a quando la palla si ferma (T1). La Quarta Dimensione è semplicemente il tempo in relazione allo spazio ed al conseguente cambiamento.
La quarta dimensione è l'insieme delle due situazioni T e T+1 in cui la palla occupa due punti diversi dello spazio a tre dimensioni. Ogni punto dello spazio a quattro dimensioni è quindi individuato univocamente dalle coordinate (X, Y, Z, T) dove 'T' sta normalmente ad indicare l'istante temporale. Il corpo (la palla) è lo stesso ed occupa nel tempo due punti diversi dello spazio a tre dimensioni. Se esiste una dimensione rappresentata dal tempo è logico presupporre che tutto ciò che è governato dal cambiamento e dalla trasformazione, e cioè tutta la fisicità in cui noi esistiamo, è una strada che perpetua nella trasformazione stessa e per propria natura temporale non finisce.
Il passare del tempo è il presupposto logico continuativo che viviamo in una dimensione passeggera appunto "di cambiamento", se ciò non fosse vero non esisterebbe il fluire del tempo come quarta dimensione.
"Le concezioni di spazio e di tempo che desidero esporvi sono sorte dal terreno della fisica sperimentale, e in ciò sta la loro forza. Esse sono fondamentali. D'ora in poi lo spazio di per se stesso o il tempo di per se stesso sono condannati a svanire in pure ombre, e solo una specie di unione tra i due concetti conserverà una realtà indipendente."
(Hermann Minkowski)


 back to top
back to top